Differences Between Diminished and Minor Intervals

If you’ve spent any time learning the basics of music theory, it’s likely that you’ve heard or seen the words diminished and minor. To the novice, these words seem like they would have similar meanings. However, these two words have very different definitions when it comes to describing music intervals.

A diminished interval is the result of a minor or perfect interval that has been lowered by one half step without a change in its interval number. A minor interval is the result of a major interval that has been lowered by one half step without a change in its interval number.

From these definitions of diminished intervals and minor intervals, one can interpret that each new interval is the result of descending one semitone from a starting interval. So if you know the starting interval and a few rules for renaming intervals when lowering them by one half step, it will be easy to distinguish the difference between diminished intervals and minor intervals.

Note: Half step can be used interchangeably with semitone.

Naming Intervals

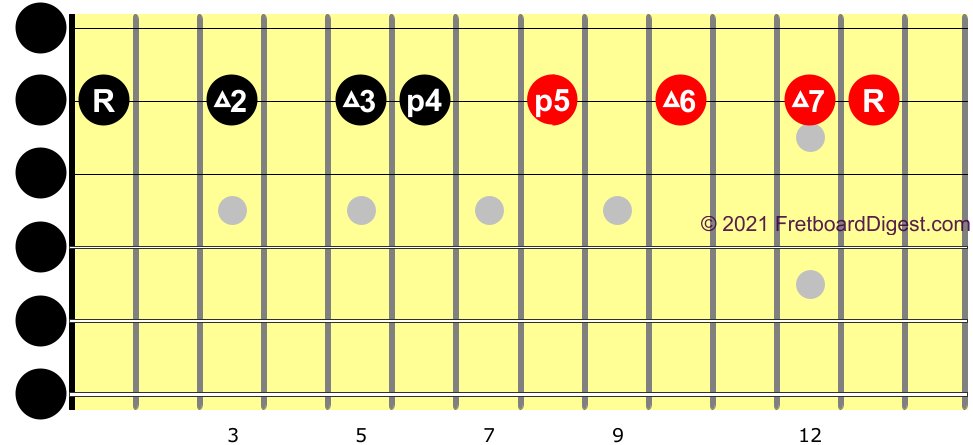
An interval’s name is formed by its quality and degree. For example, in a minor third, minor is the interval’s quality and third is the interval's degree.

The quality in an interval’s name is simply how an interval sounds. Diminished intervals (d5, d7) sound unstable or dissonant. And the sound of minor intervals can be either consonant (m3, m6) or dissonant (m2, m7), but all minor intervals have a sad or dark sound.

An interval doesn’t get the degree number in its name from its size in half steps but rather from the order of note names. For instance, in the key of C, G is five letters away from C; therefore, G forms a perfect fifth interval from the root note of C. Staying in the key of C, a diminished fifth is a G♭, not an F♯, because F is four letters away from C. With F as the fourth letter or note in the key of C, a fifth interval cannot be formed between these two letters of the musical alphabet. Any interval between C and F will be a fourth.

So in any seven-note scale, each letter of the musical alphabet is used only once. The used-only-once rule also applies to the interval numbers or degrees of a scale. Therefore, interval number can be used interchangeably with either scale degree or letter. For example, in the key of C:

interval number (5) = scale degree (fifth) = letter (G)

This used-only-once rule is the reason a diminished interval number or minor interval number isn’t changed when lowered a half step from its starting interval.

Starting Intervals

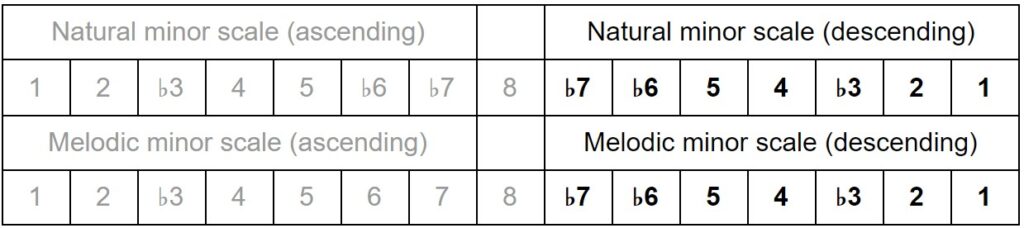
In Western music, there are twelve intervals per octave described by quality and degree. The interval quality can be described as either perfect, minor, major, diminished, or augmented. And within an octave, the interval degrees are unison, second, third, fourth, fifth, sixth, seventh, and octave.

Here are a few rules that will apply when trying to determine whether an interval will become diminished or minor when lowered by one half-step:

To Diminish

• If your starting interval is minor, decreasing the interval size by one half step will create a diminished interval, as long as there is no change in interval degree or number.
• If your starting interval is perfect, decreasing the interval size by one half step will create a diminished interval, as long as there is no change in interval degree or number.

Exception: One cannot decrease the interval size of a perfect unison. Therefore, there is no such thing as a diminished unison.

Note: Diminished is most often used to describe a diminished fifth interval and a diminished seventh interval.

To Make Minor

• If your starting interval is major, decreasing the interval size by one half step will create a minor interval, as long as there is no change in interval degree or number.

Here’s a depiction of what starting intervals become once lowered by one half step:

Table of Diminished Intervals and Minor Intervals

Adhering to the above rules, the following table will list starting intervals that are either minor, major, or perfect. However, the perfect unison will not be listed as a starting interval because there is no such thing as a diminished unison.

Note: This table references only simple intervals or intervals that are less than one octave apart.

*Enharmonically equivalent to a Perfect Unison. For example, E to F♭ is a diminished second, but its sound is enharmonically identical to the perfect unison of E to E.

**Enharmonically equivalent to a Major Seventh interval. For example, C to C♭ is a diminished octave, but its sound is enharmonically identical to the major seventh interval of C to B.

A diminished octave interval would have notes of the same letter name, but each note of the interval would have different accidentals. For instance, in the key of C, C♮ to C♭ would be a diminished octave interval.

So what about a diminished unison? While an augmented unison exists, there is no such thing as a diminished unison. Let’s use a mathematical model to explain why.

Numbers can be either positive, negative, or zero. Here’s a number line to demonstrate that:

In mathematical terms, any positive or negative number’s distance from zero is that number’s absolute value. The distance from zero (0) to negative one (-1) or from zero (0) to positive one (+1) has an absolute value of one (1).

Intervals aren’t often thought of as positive or negative; however, an interval’s distance can only be positive, unless it’s a perfect unison then the distance between its two notes is zero. So in comparison to a number line, think of an interval’s size or distance in terms of absolute value.

Middle C to middle C is a perfect unison. If one note of this perfect unison interval is lowered by one half step yet remains the same letter or degree (C♭ or unison in this case), it becomes an augmented unison. This is because the distance between the two notes is a positive distance.

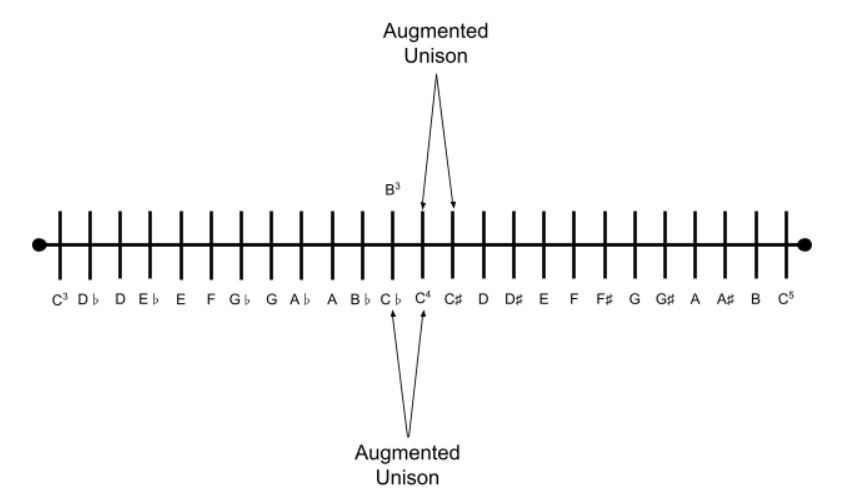
Note: C♭ is the enharmonic equivalent of B. However, the interval formed between B³ to C⁴ (middle C) is a minor second, not an augmented unison. B³ to C⁴ (middle C) is a minor second interval because there is a difference in the letter names of these two notes.

Conclusion

To recapitulate, if lowering a major interval by one half step, the new interval becomes minor, as long as there is no change in the interval number.

If lowering a minor or perfect interval by one half step, the new interval becomes diminished, as long as there is no change in the interval number.

And remember, there is no such thing as a diminished unison.

Diatonic Intervals Defined

Diatonic is a word derived from two parts: Di is a prefix borrowed from the Greek language that means double, twice, or two, whereas tonic is the first degree of a music scale. And an interval is the distance between two notes. But what does diatonic mean when it’s used as an adjective to describe music intervals?

A diatonic interval is an interval between any two music notes of a diatonic scale. A diatonic scale is a seven-note, Western music scale that has two characteristics:

1. It is composed of five whole steps (tones) and two half steps (semitones).
2. The five whole tones (whole steps) and two semitones (half steps) form two tetrachords separated by a whole tone.

A tetrachord is a series of four notes with the intervals of whole step, whole step, half step. In the C major scale example, above, one tetrachord is in black, while the second tetrachord is in red; the two tetrachords are separated by a whole step between p4 and p5.

Since diatonic intervals can exist between any two music notes of a diatonic scale, there are more diatonic intervals than the five whole steps and two half steps that make up the diatonic scale.

Note: Whole step can be used interchangeably with whole tone, whereas half step can be used interchangeably with semitone.

W = Whole step = T = whole Tone

H = Half step = S = Semitone

Naming Intervals

Music students initially learn that there are two types of diatonic intervals within an octave of the major scale: major and perfect. And they’ll learn that within that octave, there are eight intervals described by quality and degree:

Quality	Degree	Description
Perfect	Unison	two notes of the same pitch played at the same time
Major	Second	two notes, one whole step apart
Major	Third	two notes, two whole steps apart
Perfect	Fourth	two notes, two and a half steps apart
Perfect	Fifth	two notes, three and a half steps apart
Major	Sixth	two notes, four and a half steps apart
Major	Seventh	two notes, five and a half steps apart
Perfect	Octave	two notes, six whole steps apart

These eight intervals usually describe the second note’s distance from the root note in a major scale. However, one can use a diatonic interval from this list to describe the interval between any two notes of a diatonic scale, as long as that interval fits between the two notes. For example, the interval between a perfect fourth and a perfect fifth is a major second.

Each of the five whole tones within a diatonic scale is a major second interval. One interval not in the above list is the minor second interval. Each of the two semitones within a diatonic scale is a minor second interval. Therefore, add minor to the list of interval qualities: major, minor, and perfect.

The natural minor scale is a commonly used diatonic scale (described below) that has three other minor diatonic intervals: minor third, minor sixth, and minor seventh.

Though not very common, there are two other diatonic intervals found in some modes (see below) of the major scale: an augmented fourth and a diminished fifth.

Diatonic Scales

Since a diatonic interval is an interval between any two notes of a diatonic scale, let’s determine what scales are diatonic scales.

The most commonly used scales in Western music are the major scale, the three minor scales (natural, harmonic, melodic), the pentatonic scale, and the blues scale. There are many other scales, but for an introduction to diatonic intervals, only the most common are covered here.

Major

The major scale can be played in seven different modes: Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian. An oversimplified way to think of modes is to consider a major scale (Ionian) starting on its root note, while the other six modes of the major scale start on a different note or degree of the major scale.

All seven modes of the major scale contain diatonic intervals because all seven scales have five whole tones and two semitones that form two tetrachords separated by a whole tone.

For example, here are the seven modes of C major:

Ionian

C

D

E

F

G

A

B

C

D

E

F

G

A

B

Dorian

C

D

E

F

G

A

B

C

D

E

F

G

A

B

Phrygian

C

D

E

F

G

A

B

C

D

E

F

G

A

B

Lydian

C

D

E

F

G

A

B

C

D

E

F

G

A

B

Mixolydian

C

D

E

F

G

A

B

C

D

E

F

G

A

B

Aeolian

C

D

E

F

G

A

B

C

D

E

F

G

A

B

Locrian

C

D

E

F

G

A

B

C

D

E

F

G

A

B

Note: There is a more detailed description of modes, but that is beyond the scope of an introduction to diatonic intervals.

Natural Minor

The natural minor scale (Aeolian mode) is a common scale, and it is one of the seven modes of the major scale. It can be created by using the sixth degree of the major scale as the tonic or root note. And it is a diatonic scale containing diatonic intervals.

Here’s an example of E natural minor compared to G major:

Harmonic Minor

The harmonic minor is a seven-note scale, but it is not composed of five whole tones and two semitones that form two tetrachords separated by a whole tone. Therefore, it is not a diatonic scale by definition.

The intervals of the harmonic minor scale are shown, below:

Tonic (1) - W - 2 - H - ♭3 - W - 4 - W - 5 - H - ♭6 - W+H - 7 - H - (8) Octave

The Whole plus Half step (W+H) interval between the ♭6 and major 7 is also known as an augmented 2nd. This interval gives the harmonic minor a very unique sound.

Note: Some music theorists will argue that a diatonic scale is a seven-note scale with a tonal center, in which the other six scale notes move towards or away from the tonic. This argument would include the harmonic minor and ascending melodic minor (described, below) as diatonic scales.

Melodic Minor

The ascending and descending scales of melodic minor do not have the same intervals. When some musicians refer to melodic minor, they’re only thinking of the ascending scale. The ascending melodic minor is a seven-note scale, and it is composed of five whole steps and two half steps. However, it does not form two tetrachords separated by a whole tone. Therefore, it is not a diatonic scale, as defined here.

Here are the intervals of the ascending melodic minor scale:

Tonic (1) - W - 2 - H - ♭3 - W - 4 - W - 5 - W - 6 - W - 7 - H - (8) Octave

What about the descending version of the melodic minor scale?

Starting on the octave (8), here are the intervals of the descending melodic minor scale:

Octave (8) - W - ♭7 - W - ♭6 - H - 5 - W - 4 - W - ♭3 - H - 2 - W - (1) Tonic

The descending melodic minor scale is composed of five whole tones and two semitones arranged to form two tetrachords separated by a whole tone. Therefore, it is a diatonic scale composed of diatonic intervals.

Notice that the descending melodic minor scale is the same as the descending natural minor scale. This is why some musicians won’t call it a descending melodic minor scale.

To see the descending similarity, here’s a table comparing the natural minor scale to the melodic minor scale:

Pentatonic

The pentatonic scale is formed from the major scale; therefore, it has diatonic notes. However, it is a five-note scale, so it is not a diatonic scale.

Blues

The blues scale is a six-note scale, and it’s based on the pentatonic scale. Five of its six notes are diatonic notes; the additional note - the flattened fifth - is a chromatic note or passing tone. Regardless, being a six-note scale, it is not a diatonic scale.

Summary

So if a seven note scale has five whole tones and two semitones that form two tetrachords separated by a whole tone, it has diatonic intervals. But if you hear a musician using diatonic to describe the intervals of harmonic minor or ascending melodic minor, just know that he or she subscribes to a looser definition of diatonic intervals as the intervals of any seven note scale with a tonal center.